Calculating percentages is a common task in everyday life. Whether you are checking discounts, exam scores, or financial data, percentages are everywhere. Learning how to calculate percentages is simple if you understand the basic formula. This guide provides step-by-step methods, examples, and tips to simplify percentage calculations.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100, making it easier to compare values. The term “percent” originates from the Latin phrase “per centum,” meaning “per hundred.” For instance, 50% simply means 50 out of 100. Percentages are often used to show proportions, ratios, or changes in a standardized form. They are widely applied in mathematics, finance, statistics, and daily life situations, such as calculating discounts or exam scores. By converting numbers into percentages, we can better understand and compare different values regardless of their original scale.
Why Do We Use Percentages?
Percentages make it easy to compare values of different scales. For example, instead of saying “50 out of 200” or “25 out of 100,” we can use percentages like 25% to express the ratio clearly. Some common uses include:
- Calculating discounts during sales.
- Finding marks or grades in exams.
- Comparing population growth rates.
- Analyzing financial data and interest rates.
- Measuring progress or performance.
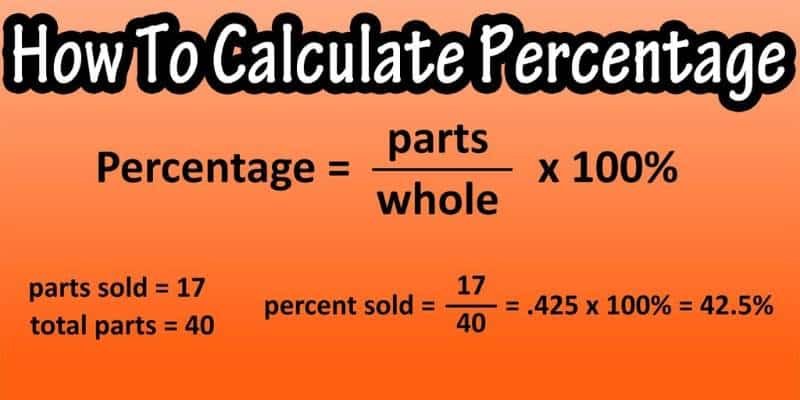
The Basic Percentage Formula
The formula for calculate percentage is:
Percentage (%) = (Part / Whole) × 100
- Part: The value you are measuring.
- Whole: The total or overall value.
For example, if you scored 40 out of 50 marks in a test:
Percentage = (40 / 50) × 100 = 80%
Step-by-Step Guide to Calculate Percentage
Follow these simple steps to find a percentage:
Step 1: Identify the Part and Whole
Determine the portion (part) and the total value (whole). For example, 30 out of 40 students passed.
Step 2: Divide the Part by the Whole
Divide 30 (part) by 40 (whole):
30 ÷ 40 = 0.75
Step 3: Multiply by 100
Multiply 0.75 by 100 to convert it into a percentage:
0.75 × 100 = 75%
Common Methods to Calculate Percentage
1. Using Fractions
If you have a fraction, convert it into a percentage by multiplying it by 100.
Example: 3/4 × 100 = 75%
2. Using Decimals
If the value is in decimal form, simply multiply it by 100.
Example: 0.6 × 100 = 60%
3. Reverse Percentage
Sometimes you know the percentage and the whole, but want to find the part. Use this formula:
Part = (Percentage × Whole) ÷ 100
Example: What is 20% of 150?
(20 × 150) ÷ 100 = 30
Tips for Quick Percentage Calculations
- Use mental math: 10% of a number is easily found by dividing by 10.
- Find 1% first: Divide by 100 to find 1%, then multiply for the required percentage.
- Break into smaller parts: For 15%, find 10% and 5% separately, then add.
Calculating Percentage Increase or Decrease
Percentage increases and decreases are very common in finance and daily life.
Percentage Increase = [(New Value – Original Value) ÷ Original Value] × 100
Percentage Decrease = [(Original Value – New Value) ÷ Original Value] × 100
Example:
A stock price rises from $100 to $120.
[(120 – 100) ÷ 100] × 100 = 20% increase.
How to Convert a Number to a Percentage?
Sometimes you need to convert a number into a percentage. For example, to convert 0.25 to a percentage:
0.25 × 100 = 25%
Similarly, 2.5 as a percentage is:
2.5 × 100 = 250%
Percentage in Exams and Results
Students often calculate their percentage from exam scores. The formula is:
Percentage = (Marks Obtained ÷ Total Marks) × 100
Example:
If you scored 320 marks out of 400:
(320 ÷ 400) × 100 = 80%
Percentage in Financial Calculations
Percentages play a major role in finance. They are used to calculate interest, tax rates, or profit margins.
Example:
If a bank offers 5% annual interest on $1000:
Interest = (5 × 1000) ÷ 100 = $50
Difference Between Percentage and Percentage Points
It is essential to understand that a percentage point and a percentage are not the same thing, even though they sound similar. A percentage point is simply the numerical difference between two percentage values. For example, if something increases from 20% to 30%, the difference is 10 percentage points. However, the percentage increase in this case is calculated relative to the original value. Moving from 20% to 30% means the value has increased by 50% of its original amount because the increase (10) is half of the starting value (20). This distinction is crucial when analyzing data, interest rates, or financial growth, as mixing them up can lead to confusion or incorrect conclusions
Conclusion
Percentages simplify comparisons and calculations in everyday life. Whether calculating discounts, exam scores, or financial growth, understanding percentages is essential. The basic formula (Part ÷ Whole) × 100 is the foundation of all percentage calculations. With practice, you can quickly solve percentage problems without difficulty.